约瑟夫环(366,约瑟夫环)
问题来源:
据说著名犹太历史学家 Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决?Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
一,留下K-1个
41数字太大了,我们就以7为例,来画个图看一下
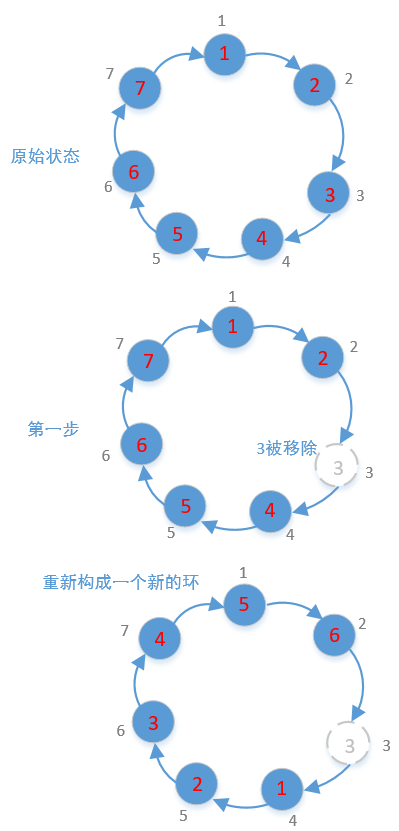




我们再来看下代码
1,数组的实现

1,3-9行表示如果k大于count就直接把所有人的编号都返回即可,不再删除了。
2,11-13行生成从1到count的所有值(包含1和count)
3,16行number统计数量,在第22-25行如果统计的数量是k的倍数就把他移除。其实我们也可以在22行成立的时候让number重新归0。这里使用的是对k求余也是可以的。
4,我们就用上面已知的两组数据测试一下,当count等于41的时候结果是16和31,当count等于7的时候结果是1和4

运行结果是

结果完全正确。
数组的删除会导致后面的元素都会往前移,频繁的删除效率肯定不是很高,其实我们还可以使用链表。因为链表的删除不需要移动后面的元素,效率还是比较高的。如果不使用链表,我们还可以把数组中删除的元素用一个负数来填充,这样也是可以的。我们来看下
2,数组实现的另一种方式

第35行该删除的我们没有删除,直接把他变为-1。在29行统计的时候如果为负数表示已经被删除了,就直接跳过,执行下一轮循环。第42-45行把最后没有被删除的放到数组live中。
3,链表实现
一般来说链表的断开要比数组的删除效率要高一些,因为数组删除某个元素之后,它后面的元素都还要往前移。使用链表会更简单一些,我们可以把它想象为一圈人大家都手牵着手,然后再一个个报数,当报到k的时候就自动退出,退出的时候左右两边人的手要牵到一块重新构成一个新的环,代码很简单,我们看下

队列实现:
除了上面说的数组和链表以外,我们还可以使用队列。这个实现起来也非常简单。我们把所有的元素全部入队,然后再一个个出队,出队的时候记录出队的个数,如果不是第k个就让他重新入队,如果是第k个就不用了入队了,然后下一个出队的再重新从1开始计算。我们还是以7来画个图看一下。



我们先来看一下代码,队列就是用之前写的359,数据结构-3,队列中的双端队列。

二,只留下一个
上面我们讲的是每到第K个删除,如果count大于等于k的话,最终会留下k-1个。但对这题还有另一个版本,就是无论多少个,最后只留下1个,就是说如果数量小于k个的时候我们继续循环删除,直到留下最后一个的为止。原理和上面非常类似,只不过当删除到最后小于K个的时候我们还要继续循环即可。图就不再画了,我们就用最后双端队列这种实现来改一下。
1,双端队列解决

2,递归解决
我们用f(n,k)表示有n个人,第k个出列,最后列出的人的编号。
那么f(n-1,k)就表示有n-1个人,第k个出列,最后列出的人的编号。
所以我们可以找到递归的公式f(n,k)=f(n-1,k) k;也就是说n-1个人组成的环相对于n个人组成的环相当于顺时针旋转了k个单位。因为是环形的,当超出环的大小的时候我们要对它求余,所以为了防止越界问题我们要这样写f(n,k)=(f(n-1,k) k)%n。
当f(1,k)的时候就表示剩下最后一个元素了,我们直接返回即可。
我们来看下代码

因为人的编号是从1开始的,所以这里要加1。当然我们还可以再来改一下,这样就不用在加1,就可以直接返回了。

3,非递归写法
看明白了上面的递归的思路,我们还可以把它改为非递归的写法

他的原理是这样的,从前往后推,如果当n=i的时候,最终留下的是m,那么当n=i 1的时候,最终留下的就是m k,考虑到m k可能大于环的长度,所以要对m k进行求余,结果就是(m k)%i,一直循环到i等于n就是最终结果。
总结:
这题只要是学过编程的大多数应该都听过,无论是使用数组,链表,还是队列都很容易解决,具有一定的代表性,希望大家能够熟练掌握。
想了解更多数据结构以及算法题,可以关注微信公众号“数据结构和算法”
(*>.<*)